1.- TANGENCIAS
1.1.- Definición de tangencia y utilidad.
Se llama recta tangente, a la recta que toca a una circunferencia (o arco de circunferencia) en un único punto, llamado punto de tangencia. Análogamente, dos circunferencias son tangentes si se tocan en un único punto.
A. Entre rectas con circunferencias
B. Entre circunferencias conociendo el radio
C. Entre circunferencias sin conocer el radio
Las tangencias permiten resolver muchos problemas geométricos y son útiles en el diseño de objetos, diseños gráficos y diseños decorativos.
1.2.- Propiedades de las tangencias.
a) Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros
b) Si una recta es tangente a una circunferencia, el radio en el punto de tangencia es perpendicular a la tangente.
c) El centro de cualquier circunferencia tangente a dos rectas se encuentra en la bisectriz del ángulo que forman.
d) El centro de cualquier circunferencia que pase por dos puntos está en la mediatriz del segmento.
1.3.- Casos de tangencias:
 1º.- RECTAS TANGENTES A UNA CIRCUNFERENCIA DESDE UN PUNTO EXTERIOR (aquí el enlace con el proceso en youtube).
1º.- RECTAS TANGENTES A UNA CIRCUNFERENCIA DESDE UN PUNTO EXTERIOR (aquí el enlace con el proceso en youtube).OPERACIONES:
- Se unen los puntos P y Oc y se halla el punto medio de este segmento. Se optiene OT.
- Haciendo centro en OT, se traza una circunferencia que pase por P y por Oc, cortando a la circunferencia original en T1 y T2 (puntos de tangencia).
- Se trazan dos rectas que pasen por P y por T1 y T2. Son las rectas tangentes a la circunferencia dada.
2º - RECTAS TANGENTES EXTERIORES A DOS CIRCUNFERENCIAS (aquí el enlace con el proceso en youtube)
OPERACIONES:
- Se unen los puntos O1 y O2 y se halla el punto medio de este segmento. Se optiene O3.
- Haciendo centro en O3, se traza una circunferencia que pase por los centros O1 y O2.
- Desde O2 (circunferencia mayor) y con el radio R2-R1, se traza una circuferencia. Se obtienen los puntos 1 y 2.
- Desde O2 se trazan rectas que pasen por 1 y 2. Se obtienen T1 y T2.
- Desde O1, trazar paralelas a las anteriores y se obtienen T3 y T4.
- Unir T3-T1 y T4-T2.
3º.- RECTAS TANGENTES INTERIORES A DOS CIRCUNFERENCIAS (aquí el enlace con el proceso en youtube)
OPERACIONES:
- Se unen los puntos O1 y O2 y se halla el punto medio de este segmento. Se optiene O3.
- Trazar una circunferencia (de centro en O3) pasando por O1 y O2.
- Desde O2 y con el radio R2+R1, se traza una circuferencia. Se obtienen los puntos 1 y 2.
- Desde O2 se trazan rectas que pasen por 1 y 2. Se obtienen T1 y T2.
- Desde O1, trazar (en sentido contrario) paralelas a las anteriores y se obtienen T3 y T4.
- Unir T3-T1 y T4-T2.
4º.-CIRCUNFERENCIA DE RADIO CONOCIDO TANGENTE A DOS RECTAS QUE SE CORTAN
Aquí en el dibujo tienes una versión simplificada. Falta señalar el punto de tangencia de la circunferencia con la recta r, con un radio perpendicular a ella. Entra en el enlace de abajo y verás qué bien te lo explican.
5º. CIRCUNFERENCIAS DE RADIO CONOCIDO TANGENTES A UNA CIRCUNFERENCIA Y UNA RECTA DADAS
Siendo r el radio de las circunferencias tangentes a la circunferencia y la recta s dadas:
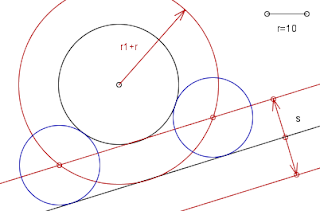
Observa el proceso aquí en el vídeo y lee abajo las instrucciones, te ayudará.
|
- Trazamos la circunferencia de radio r1+r (r1 es el radio de la circunferencia dada), y las rectas paralelas a s que disten de ella una distancia igual al radio r
- Los puntos comunes a ambos son los centros de las circunferencias buscadas. Sólo falta señalar en este ejemplo, los puntos de tangencia exactos (unión de los centro, y radios perpendiculares a la recta s).
- Si los datos lo permiten, también es posible hallar los centros de dos circunferencias tangentes interiores a la dada, restando los radios r1-r.
- Atención: Para acabar el ejercicio en el ejemplo superior falta señalar con exactitud los puntos de tangencia, que se hallan uniendo los centros (los cuales también han olvidado nombrar, como ves es algo importante para referirnos a los elementos, pero no encontré otra imagen mejor).
+de+CIMG7337.JPG) |
| Aquí un ejemplo con tres latas tangentes entre sí, aunque la verdad es que no las han juntado bien del todo y parece que el punto "t " rellena el hueco...pero se entiende la propuesta, ¿no?. |
Para ello, si haces un esquema de cómo quedaría la solución, observarás que los centros de las tres circunferencias forman un triángulo. Debes construir ese triángulo escaleno, con ayuda del compás, cuyos lados miden la suma de dos radios, por parejas: r1+r2, r1+r3 y r2+r3. Dibuja primero cada segmento suma, para llevarlos con el compás y ver dónde se cortan.
Ten cuidado de seguir bien el esquema previo para ordenar bien cada circunferencia. Cómo ves en esos lados del triángulo ya tienes situados los puntos de tangencia entre cada pareja también, donde acaba cada radio sumado con el siguiente. Y al final trazas las tres circunferencias solución.
7º CONSTRUIR CIRCUNFERENCIAS DE RADIO CONOCIDO TANGENTES A OTRA CIRCUNFERENCIA DADA Y QUE PASEN POR UN PUNTO EXTERIOR "P".
- Para hallar las circunferencias de radio R conocido que pasando por un punto P dado son tangentes a una circunferencia dada de centro C y radio r, se trazará una circunferencia con centro en P y radio R y otras dos circunferencias con centro en C y radios R+r y r-R, respectivamente.
- Los puntos de intersección de dichas circunferencias serán los centros de las circunferencias que pasando por P y siendo tangentes a C tienen radio R.
- Los puntos de intersección situados sobre la circunferencia de radio R+r se corresponden con los centros de las circunferencias que son tangentes exteriores a C, mientras que los puntos de intersección situados sobre la circunferencia de radio r-R se corresponden con los centros de las circunferencias que son tangentes interiores a C.
- La circunferencia de centro P y radio R podrá ser secante, tangente o no cortar a las circunferencias de radio R+r y de radio r-R, pudiendo existir 1, 2, 3, 4 o ninguna solución al problema (como mucho habrá dos circunferencias tangentes interiores a C y dos circunferencias tangentes exteriores a C que pasan por P y tienen radio R). En este dibujo del ejemplo sólo tiene como solución las dos circunferencias tangentes exteriores, porque la de centro C y radio r - R no se corta con la otra de centro en P.
- Atención: Para acabar el ejercicio en el ejemplo superior falta señalar con exactitud los puntos de tangencia, que se hallan uniendo los centros O1 con C y O2 con C.
2.- ENLACES
Si es entre dos circunferencias tangentes nos quedamos con el trozo de curva que enlaza una con otra y borramos el resto.
Si el enlace es entre recta y curva, entonces borramos la parte de la curva que no va unida a la recta tangente a ella.
EJERCICIO: CÓMO ENLAZAR PUNTOS MEDIANTE CURVAS.
Aquí tienes dos webs con ejemplos resueltos de este ejercicio:
http://www.slideshare.net/qvrrafa/tema-5-tangencias-y-enlaces-presentation (ver la diapositiva 35)
http://laverdaderamagnitud.wordpress.com/geometria-plana/ (en el apartado TANGENCIAS, ver el punto 3)










No hay comentarios:
Publicar un comentario